| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- level 2
- pandas
- oracle
- level 1
- 카카오
- R
- seaborn
- 머신러닝
- matplotlib
- 데이터 분석
- Oracel
- Kaggle
- 프로그래머스
- 튜닝
- 빅데이터 분석 기사
- 실습
- sklearn
- Python
- 오라클
- SQL
- python3
- 실기
- Numpy
- 코딩테스트
- 빅분기
- 파이썬
- 알고리즘
- Today
- Total
라일락 꽃이 피는 날
[빅분기 실기] 군집 분석 (Cluster Analysis) 본문
군집 분석 (Cluster Analysis)
개체들의 특성을 대표하는 몇 개의 변수들을 기준으로 몇 개의 군집으로 세분화하는 방법
개체들을 다양한 변수를 기준으로 다차원 공간에서 유사한 특성을 가진 개체로 묶는다.
개체들 간의 유사성은 개체 간의 거리를 사용하고, 거리가 상대적으로 가까운 개체들을 동일 군집으로 묶는다.
개체 간의 거리를 행렬을 이용하여 계산한다. 대표적으로 유클리디안 거리를 계산한다.
[주요 하이퍼파라미터]
- n_cluster : 군집의 수
1. 군집분석 (Clustering)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm
from sklearn.cluster import KMeans
plt.style.use('seaborn-deep')
cmap = matplotlib.cm.get_cmap('plasma')data = pd.read_csv('Mall_Customers.csv')
X = data.iloc[:, [3,4]]
X.head()
wcss = []
for i in range(1,21):
kmeans = KMeans(n_clusters=i)
kmeans.fit_transform(X)
wcss.append(kmeans.inertia_)wcss
통계 기준으로 최적의 군집수를 찾기 위한 과정이다.
kmeans.inertia_ : 군집의 중심과 각 케이스(개체) 간에 거리를 계산한다.
중심과 개체 간의 거리가 작아진다는 것은 그만큼 군집이 잘 형성이 되었다는 것이다.
plt.figure()
plt.plot(range(1,21), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
군집수가 늘어날수록 수치가 작아지고 있다.
수치가 크게 감소하다가 변화가 없는 지접에서 최적의 군집수 k를 결정한다.
k = 5
kmeans = KMeans(n_clusters = k)
y_kmeans = kmeans.fit_predict(X)
y_kmeans
Group_cluster=pd.DataFrame(y_kmeans)
Group_cluster.columns=['Group']
full_data=pd.concat([data, Group_cluster], axis=1)
full_data
kmeans_pred = KMeans(n_clusters=k, random_state=42).fit(X)
kmeans_pred.cluster_centers_
cluster_centers_ : 각 좌표의 중심점 결과가 담겨져 있는 객체
군집의 중심좌표로 군집의 특성을 살펴보고, 이들 간에 직관적으로 명확한 분리가 되어야 제대로 된 군집수를 나눈 것으로 본다.
labels = [('Cluster ' + str(i+1)) for i in range(k)]
X=np.array(X)
plt.figure()
for i in range(k):
plt.scatter(X[y_kmeans == i, 0], X[y_kmeans == i, 1], s = 20,
c = cmap(i/k), label = labels[i])
2차원 도표에 산점도(scatter plot)를 그린다.
for문으로 각 개체만큼 하나씩 y_kmeans에 분석하여 저장된 좌표값을 찍는다.
라벨에 따라 색을 다르게하기 위해 label = labels[i] 로 설정한다.
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
s = 100, c = 'black', label = 'Centroids', marker = 'X')
plt.xlabel('Income')
plt.ylabel('Spend')
plt.title('Kmeans cluster plot')
plt.legend()
plt.show()
중심좌표 결과(kmeans.cluster_centers_)를 이용하여 각 군집의 중심점만 찍는다.
plt.figure()
for i in range(k):
plt.scatter(X[y_kmeans == i, 0], X[y_kmeans == i, 1], s = 20,
c = cmap(i/k), label = labels[i])
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
s = 100, c = 'black', label = 'Centroids', marker = 'X')
plt.xlabel('Income')
plt.ylabel('Spend')
plt.title('Kmeans cluster plot')
plt.legend()
plt.show()
각 개체의 좌표와 군집 중심의 좌표를 한 도표에 표현한다.
2. K-mean Clustering
분석 속도가 빠르고 군집을 형성하면서 유연하게 다른 군집으로 다시 재군집화가 가능하다.
from scipy.spatial.distance import cdist, pdist
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
iris = pd.read_csv("iris.csv")
print (iris.head())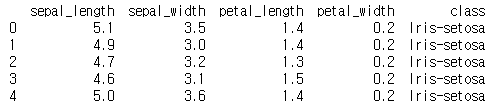
sepal_length : 꽃받침의 길이 / sepal_width : 꽃받침의 넓이
petal_length : 꽃잎의 길이 / petal_width : 꽃잎의 넓이
class : 꽃의 종류 (3종류)
x_iris = iris.drop(['class'],axis=1)
y_iris = iris["class"]군집분석은 레이블이 있으면 안 되기 때문에 class 변수는 drop 한다.
추후 분류가 잘 되어있는지 확인하기 위해 y_iris 에 담는다.
x_iris.describe()
4개의 변수 단위가 달라서 평균에 차이가 있고, 최댓값과 최솟값도 다르다.
개체들 간의 거리를 계산할 때 단위 때문에 더 다르거나 비슷하게 될 수 있다.
따라서 데이터 단위의 정규화가 필요하다.
from sklearn.preprocessing import StandardScaler
scale=StandardScaler()
scale.fit(x_iris)
X_scale=scale.transform(x_iris)
pd.DataFrame(X_scale).head()
데이터를 표준화하여 X_scale 이라는 데이터셋에 담고, 다시 기술 통계를 확인한다.
K = range(1,10)
KM = [KMeans(n_clusters=k).fit(X_scale) for k in K]
centroids = [k.cluster_centers_ for k in KM]
D_k = [cdist(x_iris, centrds, 'euclidean') for centrds in centroids]
cIdx = [np.argmin(D,axis=1) for D in D_k]
dist = [np.min(D,axis=1) for D in D_k]
avgWithinSS = [sum(d)/X_scale.shape[0] for d in dist]유클리디안(euclidean) 방법으로 거리를 계산하여 D_k에 담는다.
계산한 거리 중 최솟값(np.argmin) 을 cIdx 에 담고, dist 로 최솟값을 구한다.
argWithinSS 은 군집의 중심과 개체들 간의 최소 거리들의 평균을 구하여 저장한 값이다.
wcss = [sum(d**2) for d in dist]
tss = sum(pdist(X_scale)**2)/X_scale.shape[0]
bss = tss-wcss각 군집 내에 wcss 는 개체들간의 거리를 제곱하여 더한 값이다.
tss 는 전체 개체들간의 거리를 제곱하여 개체수로 나눈 값이다.
bss 로 wcss 와 tss 의 차이를 계산한다.
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(K, avgWithinSS, 'b*-')
plt.grid(True)
plt.xlabel('Number of clusters')
plt.ylabel('Average within-cluster sum of squares')
plt.title('Elbow for KMeans clustering')
최적의 군집수를 구하기 위해 군집을 1~10 까지 변화할 때의 평균 군집내 거리(avgWithinSS)를 그린다.
군집수를 4 또는 6으로 하는 것이 적합해보인다.
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(K, bss/tss*100, 'b*-')
plt.grid(True)
plt.xlabel('Number of clusters')
plt.ylabel('Percentage of variance explained')
plt.title('Elbow for KMeans clustering')
개체들 간의 분산비율을 군집수를 달리하면서 본다.
Y축이 음수이기 때문에 0에 가까울수록 적합한 k 이다.
4~6 사이에서 군집을 결정하는 것이 적합해보인다.
import numpy as np
w,v = np.linalg.eig(np.array([[ 0.91335 ,0.75969 ],[ 0.75969,0.69702]]))
print ("\nEigen Values\n",w)
print ("\nEigen Vectors\n",v)
k_means_fit = KMeans(n_clusters=4, max_iter=300)
k_means_fit.fit(X_scale)
k_means_fit.cluster_centers_
print ("\nK-Means Clustering - Confusion Matrix\n\n",
pd.crosstab(y_iris,k_means_fit.labels_,rownames = ["Actuall"],colnames = ["Predicted"]) )
실제 3종류의 꽃(y_iris) 과 군집으로 나눈 4개의 군집 간에 일치하는지를 확인한다.
print ("\nSilhouette-score: %0.3f" % silhouette_score(x_iris, k_means_fit.labels_, metric='euclidean'))
for k in range(2,10):
k_means_fitk = KMeans(n_clusters=k,max_iter=300)
k_means_fitk.fit(x_iris)
print ("For K value",k,",Silhouette-score: %0.3f" % silhouette_score(x_iris, k_means_fitk.labels_, metric='euclidean'))
군집수를 2~10 까지 변경하면서 실루엣 스코어(silhouette-score)를 찾는다.
3. 계층적 군집분석 (Hierarchical Clustering)
한 번 어떤 군집에 속한 개체는 분석 과정에서 다른 군집과 더 가깝게 계산되어도
다른 군집화가 허용되지 않는 방법이고, 속도도 다소 오래 걸린다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm
plt.style.use('seaborn-deep')
cmap = matplotlib.cm.get_cmap('plasma')
data = pd.read_csv('Mall_Customers.csv')
X = data.iloc[:, [3,4]].values
import scipy.cluster.hierarchy as sch
plt.figure(1)
z = sch.linkage(X, method = 'ward')
dendrogram = sch.dendrogram(z)
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('ward distances')
plt.show()
개체들 간의 거리를 ward 방법으로 하고 덴드로그램을 그린다.
from sklearn.cluster import AgglomerativeClustering
k = 5
hc = AgglomerativeClustering(n_clusters = k, affinity = "euclidean", linkage = 'ward')
y_hc = hc.fit_predict(X)군집수를 5로하여 병합 군집(Agglomerative Clustering)을 적용한 군집분석을 수행한다.
시작할 때 각 포인트를 하나의 클러스터로 지정하고,
그 다음 종료 조건을 만족할 때까지 가장 비슷한 두 클러스터를 합치는 방식으로 진행한다.
labels = [('Cluster ' + str(i+1)) for i in range(k)]
plt.figure(2)
for i in range(k):
plt.scatter(X[y_hc == i, 0], X[y_hc == i, 1], s = 20,
c = cmap(i/k), label = labels[i])
plt.xlabel('Income')
plt.ylabel('Spending score')
plt.title('HC cluster plot')
plt.legend()
plt.show()
5개의 군집으로 나누어진 것을 확인할 수 있다.
'데이터 분석 > 빅데이터 분석 기사' 카테고리의 다른 글
| [빅분기 실기] 연관규칙분석 (Association Rule) (0) | 2022.06.20 |
|---|---|
| [빅분기 실기] DBSCAN (0) | 2022.06.20 |
| [빅분기 실기] 엘라스틱넷 (Elasticnet) (0) | 2022.06.19 |
| [빅분기 실기] 라쏘 (Lasso) (0) | 2022.06.19 |
| [빅분기 실기] 릿지 (Ridge) (0) | 2022.06.19 |


