Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- pandas
- R
- seaborn
- 프로그래머스
- 머신러닝
- Oracel
- SQL
- 빅데이터 분석 기사
- 파이썬
- level 2
- 실습
- 튜닝
- 빅분기
- 알고리즘
- sklearn
- 카카오
- Numpy
- 데이터 분석
- Python
- 실기
- python3
- Kaggle
- 오라클
- oracle
- 코딩테스트
- matplotlib
- level 1
Archives
- Today
- Total
라일락 꽃이 피는 날
[빅분기 실기] 라쏘 (Lasso) 본문
728x90
728x90
라쏘 (Lasso)
릿지 회귀모델과 유사하게 특성의 계수값을 0에 가깝게 하지만
실제 중요하지 않은 변수의 계수를 0으로 만들어 불필요한 변수를 제거하는 모델
[주요 하이퍼파라미터]
- alpha : 값이 클수록 계수를 0에 가깝게 제약하여 훈련 데이터의 정확도는 낮아지지만 일반화에 기여한다. (default = 1)
값이 0에 가까울수록 회귀계수를 아무런 제약을 하지 않은 선형회귀와 유사하게 적용한다.
1. 분석 데이터 준비
# 주택 가격 데이터
data2=pd.read_csv('house_price.csv', encoding='utf-8')
X=data2[data2.columns[1:5]]
y=data2[["house_value"]]
1-2. train-test 데이터셋 나누기
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test=train_test_split(X, y, random_state=42)
1-3. Min-Max 정규화
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler()
scaler.fit(X_train)
X_scaled_train=scaler.transform(X_train)
X_scaled_test=scaler.transform(X_test)
2. 기본모델 적용
2-1. 훈련 데이터
from sklearn.linear_model import Lasso
model=Lasso()
model.fit(X_scaled_train, y_train)
pred_train=model.predict(X_scaled_train)
model.score(X_scaled_train, y_train) # 0.5455724679313863
2-2. 테스트 데이터
pred_test=model.predict(X_scaled_test)
model.score(X_scaled_test, y_test) # 0.5626850497564577
① RMSE (Root Mean Squared Error)
import numpy as np
from sklearn.metrics import mean_squared_error
MSE_train = mean_squared_error(y_train, pred_train)
MSE_test = mean_squared_error(y_test, pred_test)
print("훈련 데이터 RMSE:", np.sqrt(MSE_train))
print("테스트 데이터 RMSE:", np.sqrt(MSE_test))
3. 하이퍼파라미터 튜닝
3-1. Grid Search
param_grid={'alpha': [0.0, 1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 0.1, 0.5, 1.0, 2.0, 3.0]}alpha 값을 11가지로 설정하고 그리드 탐색을 진행한다.
from sklearn.model_selection import GridSearchCV
grid_search=GridSearchCV(Lasso(), param_grid, cv=5)
grid_search.fit(X_scaled_train, y_train)
print("Best Parameter: {}".format(grid_search.best_params_))
print("Best Score: {:.4f}".format(grid_search.best_score_))
print("TestSet Score: {:.4f}".format(grid_search.score(X_scaled_test, y_test)))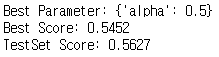
최적의 alpha는 0.5로, 이때 훈련 데이터의 정확도는 54.5%, 테스트 데이터의 정확도는 56.3% 이다.
3-2. Random Search
from scipy.stats import randint
param_distribs = {'alpha': randint(low=0.00001, high=10)}랜덤 탐색을 위해 alpha를 0.00001 ~ 10 사이의 범위에서 100번(n_iter) 무작위 추출하는 방식을 적용한다.
from sklearn.model_selection import RandomizedSearchCV
random_search=RandomizedSearchCV(Lasso(),
param_distributions=param_distribs, n_iter=100, cv=5)
random_search.fit(X_scaled_train, y_train)
print("Best Parameter: {}".format(random_search.best_params_))
print("Best Score: {:.4f}".format(random_search.best_score_))
print("TestSet Score: {:.4f}".format(random_search.score(X_scaled_test, y_test)))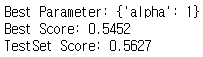
최적의 alpha는 1로, 이때 훈련 데이터의 정확도는 54.5%, 테스트 데이터의 정확도는 56.3% 이다.
728x90
'데이터 분석 > 빅데이터 분석 기사' 카테고리의 다른 글
| [빅분기 실기] 군집 분석 (Cluster Analysis) (0) | 2022.06.20 |
|---|---|
| [빅분기 실기] 엘라스틱넷 (Elasticnet) (0) | 2022.06.19 |
| [빅분기 실기] 릿지 (Ridge) (0) | 2022.06.19 |
| [빅분기 실기] 선형회귀모델 (Linear Regression Model) (0) | 2022.06.19 |
| [빅분기 실기] 앙상블 스태킹 (Stacking) (0) | 2022.06.19 |

