[빅분기 실기] 선형회귀모델 (Linear Regression Model)

선형회귀모델 (Linear Regression Model)

연속형 원인 변수가 연속형 결과 변수에 영향을 미치는지를 분석하여 레이블 변수를 예측

가장 대표적인 오차 지표인 RMSE는 실제값과 예측값 간에 전 구간에 걸친 평균적인 오차

 

 

 

 

---

 

 

1. 분석 데이터 준비

# 주택 가격 데이터
data2=pd.read_csv('house_price.csv', encoding='utf-8')

X=data2[data2.columns[1:5]]
y=data2[["house_value"]]

 

 

 

1-2. train-test 데이터셋 나누기

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test=train_test_split(X, y, random_state=42)

 

 

 

1-3. Min-Max 정규화

from sklearn.preprocessing import MinMaxScaler

scaler=MinMaxScaler()
scaler.fit(X_train)

X_scaled_train=scaler.transform(X_train)
X_scaled_test=scaler.transform(X_test)

 

 

 

 

2. Statmodel

파이썬의 통계분석 모듈

 

import statsmodels.api as sm

x_train_new = sm.add_constant(X_train)
x_test_new = sm.add_constant(X_test)
x_train_new.head()

X_train 에 상수항 변수를 더하여 x_train_new 라는 변수로 만든다.

const 변수가 상수를 추정하는 역할을 한다.

통계적 회귀분석에서는 일반적으로 X 데이터의 정규화를 하지 않는다.

 

 

 

2-1. 훈련 데이터

multi_model = sm.OLS(y_train,x_train_new).fit()
print (multi_model.summary())

R-squared: 0.546 → 54.6% 수준으로 회귀직선(예측값)과 실제값이 일치한다.

coef : 각 X 변수가 1증가할 때마다 Y가 변화하는 정도 (=기울기)

p>|t| : 통계적으로 유의한가를 검증한 결과로, 0.05보다 작으면 유의한 영향을 미치는 변수로 본다.

 

 

 

2-2. 테스트 데이터

multi_model2 = sm.OLS(y_test,x_test_new).fit()
print (multi_model2.summary())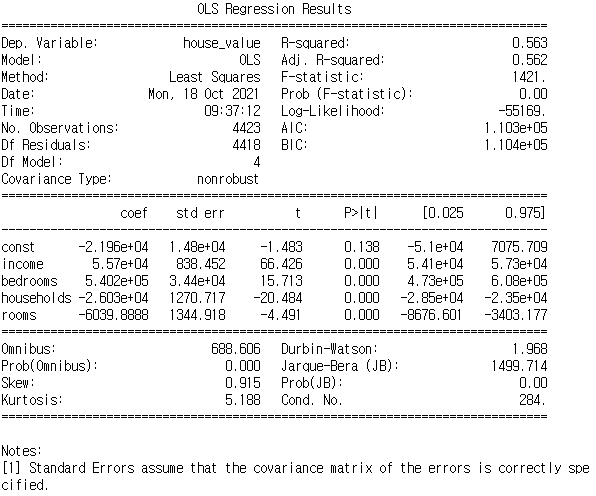

 

 

 

 

3. 기본모델 적용

 

3-1. 훈련 데이터

from sklearn.linear_model import LinearRegression

model=LinearRegression()
model.fit(X_scaled_train, y_train)

pred_train=model.predict(X_scaled_train)
model.score(X_scaled_train, y_train)  # 0.5455724996358273

 

 

 

2-2. 테스트 데이터

pred_test=model.predict(X_scaled_test)
model.score(X_scaled_test, y_test)  # 0.562684388358716

 

 

 

① RMSE (Root Mean Squared Error)

import numpy as np
from sklearn.metrics import mean_squared_error 

MSE_train = mean_squared_error(y_train, pred_train)
MSE_test = mean_squared_error(y_test, pred_test)

print("훈련   데이터 RMSE:", np.sqrt(MSE_train))
print("테스트 데이터 RMSE:", np.sqrt(MSE_test))

 

 

 

② MAE (Mean Absolute Error)

from sklearn.metrics import mean_absolute_error

mean_absolute_error(y_test, pred_test)  # 47230.874701637375

 

 

 

③ MSE (Mean Squared Error)

from sklearn.metrics import mean_squared_error 

mean_squared_error(y_test, pred_test)  # 3996869138.1105847

 

 

 

④ MAPE (Mean Absolute Percentage Error)

def MAPE(y_test, y_pred):
    return np.mean(np.abs((y_test - pred_test) / y_test)) * 100 
    
MAPE(y_test, pred_test)

 

 

 

⑤ MPE (Mean Percentage Error)

def MAE(y_test, y_pred):
    return np.mean((y_test - pred_test) / y_test) * 100
    
MAE(y_test, pred_test)